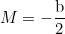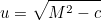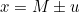Klakap wrote:That’s all! No ugly big formula!
I beg to differ. This method is known in Germany (in only slightly different form) as the midnight formula (reason being, you should be able to recite it even if awoken at midnight with no warning). I've used this way to solve quadratics all my life, certainly before 2019. And I never understood the fascination I've seen in others with the general formula. You see, in my book of formulas, there was apparently a typo in the general formula, and it was too complicated for my taste, anyway, so I just always used the normal formula.
No, if you want a novel way without a formula, you can use al-Khwarizmi's original method. Bring the equation into the form x² + px = q. Geometrically, the left hand side is an area, so the right hand side must be an area as well. In particular, the left hand side is a square of unknown side length plus a rectangle with one known and one unknown side, and that all adds up to a known area. But we can rearrange the left hand side: If we bisect the rectangle along the side p, then we get two rectangles with side lengths x and p/2. We can paste these onto the unknown square on the right and the bottom (this will go easier if you make a picture, but I have no scanner handy and my paint skills suck). Then the resulting figure is almost a square. In fact, we would only need to add a square with side length p/2 to complete a square, and we can add to the left hand side if we also add the same to the right hand side. Then on the left we have a square with side length x + p/2, and on the right we have a known area quantity: (x + p/2)² = q + p²/4. All that is left to do is to take the root and subtract the p/2 to isolate the x. And of course, in order to get both solutions, you have to put a +- in front of the square root: x = -p/2 +- sqrt(q + p²/4).