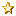Article on physical memory management

[turdus]

The question should be, why is it a problem that a structure for memory management needs like 128kb (e.g. the bitmap) for managing 4gb of ram?

The problem is, it does not scale well.

You haven´t answered the "flaws" I found in your algo.

I did. All of them.
1. 2/4mb pages: it's not to solve that problem as stack allocator does not solve it either
2. it does not crash if fifo is full
3. it does scale on number of fragments, not on the amount of RAM, little footprint
4. it does not let memory to fragment endlessly, hence keep free's O(m) small.

I think I'll simply discard you in the future until you learn to read.

[FlashBurn]

But when you use the free mem as cache, then it is not free and the pmm doesn´t need to keep track of it.

[Owen]

any memory used on these free pages does not count.

As I wrote before, I rather use that area as cache, so it does count for me.

If its cache, it's not free!

[FlashBurn]

@turdus

Your answer to my question, why your algorithm is faster when it gets to merging was:

Since it does not scale on amount of RAM. It scales on number of E820 entries.

That´s not an answer to my question. My stack approach needs for freeing O(1) (this also includes merging) and your approach needs O(n) which is slow. You are always arguing that you wont have much fragments, but as said, you can´t assure this.
I also showed you, that the algorithm you posted will produce more fragments than needed (which is for me a design flaw), because of that it is really easy to get many fragments and then a free with O(n) that can be a problem.

As I said (you should really learn reading ) my stack approach can alloc/free 4kb pages and 2/4mb pages.

it does scale on number of fragments, not on the amount of RAM, little footprint

Yeah and the number of fragments belongs to the amount of RAM (because of fragmentation) and there comes your magic defragmenter, but then your algorithm scales really bad, because the more RAM you have the more often your defragmenter will run (have you thought that this will cost performance, cache trashing and things like that?).

But one more question, you said:

it does not let memory to fragment endlessly, hence keep free's O(m) small.

Is it because of your defragmenter? As I said, this also counts to the overhead (and memory footprint) of you pmm and it makes your algorithm under heavy load even more slower.

So the only advantage you have is, that you save some time (maybe some ms) at boot and that you save some mem (something over 100kb for the bitmap, assuming 4gb RAM, and nothing for the stack), but the disadvantage is that it is slower.

[turdus]

If its cache, it's not free!

If it would be marked as used, other processes could not allocate it! I think any memory that's allocateable, should considered to be free.

I try to explain it with other words. At a given time some memory is allocated and used, some not. We can make use of this unallocated memory as a temporary disk cache, but only if it's not going to be used by any other process. If a process allocates a new page, the disk cache shrinks by that page. If a process frees a page, the disk cache grows dynamically.

But, it depends on how you design your kernel, you can take a different approach of course! This is how linux and my kernel do at least. Feel free to find out your way!

[cyr1x]

If it would be marked as used, other processes could not allocate it! I think any memory that's allocateable, should considered to be free.

When there are no pages left the pmm can just ask the cache to free some memory.

This is how linux ... do at least.

No it doesn't. Take a look at the 'free' and 'cached' columns.

[Velko]

Well, if we are talking about PMM's, take a look at mine It's a bitmap-like structure, something I call bittree.

So, instead of trying to invent a better stack, I went ahead to invent (or re-invent, I'm not sure ) a better bitmap. A bitmap, to which I added a several indexing levels.

Characteristics:

• Looking up for a free page: O(log_32(n))
• Allocating: O(log_32(n))
• Freeing: O(log_32(n))
• Checking if page is allocated or not: O(1) - a feature that really helps to catch bugs.
• Memory spent: O(n)

I don't see why spending 128KiB per 4GiB (or 0.0031%) qualifies as "too much". And if you are willing to spend slightly over 4KiB more (precisely + 4KiB + 128 + 4, frankly last 4 bytes could be omitted, but it makes implementation much clearer), you can get overall performance of O(log_32(n)). Also it can be promoted to O(log_64(n)) easely, but it really doesn't make a big difference until 64 or 128 GiB (5 levels, 6 levels, do not care), and I prefer to keep my background libraries common for 32- and 64-bit systems.

I've posted basic idea (when it was in it's infancy) here, it somewhat resembles Cottontail (mentioned before by Legendmythe) or Brendan's idea about array of "number of free 4 KiB pages" entries for each 2 MiB page, in this thread.

Here's a simplified illustration for 4-bit indexing groups: (in reality I'm using 32-bit groups, but it wouldn't be practical to draw that)

To make it clear: 1 means free page, 0 - allocated. Bit set in a upper level means that there's at least one bit set in corresponding group at lower level.

Basic algorithms

• Look up for a free page: start at a top, find first nonzero bit at that level (preferably using BSF instruction or GCC's __builtin_ctz()). Descend to next level, find a nonzero bit there, and so on until you hit the bottom.
• Allocating: clear a bit in lower level, then if a whole group becomes 0, update a bit in upper level, and so on until the top (or stop).
• Freeing: set a bit in lower level, if whole group was 0 before, update a bit in upper level and so on...
• Checking if page is allocated: just check the bit in lower level.

Start and end ranges can be applied to search easily - if something doesn't like addresses above 4 GiB, just add a limit. Something do no fear those addresses - just start searching from there first.

Support for 4 MiB pages also could be added - it just needs additional, parallel upper levels (slightly different, checking for 0xFFFFFFFF, not 0). 2 MiB pages would be trickier, as it involves 16-bit groups somewhere between 4KiB and 2 MiB, but are doable anyway.

Currently I'm using 4KiB-only version, and it works great And the whole thing is implemented in ~110 lines of C code (could be less, I'm a \n-happy guy).

[Brendan]

Hi,

You need to understand that there's 3 different (but related) quantities:

• the amount of virtual address space used

Am I right that you do not take the virtual space occupied by the now-mapped page into account for this metric?

For free page stacks?

In that case a "now-mapped" page would be classed as allocated (and no longer free, and therefore not counted in the free page stack costs).


Cheers,

Brendan

[OSwhatever]

Velko, your cottontail variant is a good approach when it comes to speed and memory requirements. Combining this with a buddy tree as well and you have a very versatile allocator. Then the memory required would be (num_pages * 4)/8 Bytes. 4GB would then consume 512KB.

[Ready4Dis]

You made my day, man!!!

A stack uses only 1 pointer. That's it.

ROTFL. PLease show me a stack implementation that uses *ONLY* a pointer. No further allocation allowed.

De-allocation is faster than O(1).

LOL, LOL, LOL. You're killing me with laught, stop it. Faster than O(1)...

I found that I tended to allocate pages 1 (or a few) at a time, but de-allocate in big chunks when processes are killed or a file is closed. If all the pages in a process are linked together, you can return the entire list with 4 pointer assignments.

Let's see: deallocate a big chunk, you have to walk next pointers as many times as big chunk is multiple of 4k. That's f*cking not faster than O(1), but O(n)!!!

My implementation only uses a single pointer... and it supports however much ram your system has. It has a pointer to the next free page, that is all. All free pages contain a pointer to another free page (aka, linked list, but the list is NEVER traversed except in the beginning when it first boots). With 100% memory allocation, my implementation takes 4-bytes (32-bit) or 8 bytes (64-bit). With no memory allocated, it takes memory, but who cares, it's all free memory anyways. Allocations are O(1), deallocations are O(1), and memory required in worst case situation is 4kb. Of course, my method ONLY supports allocated a single page at a time, so far this hasn't been an issue. I use a bitmap for sub 1mb for old school drivers, and limit them in the resources they can use, but it's not meant for old hardware, so this isn't an issue for me either. Each person has their own requirements, so just because it works in my case, doesn't mean it's the best method for everyone.

[FlashBurn]

I know that the most only code for x86, but if you want to port it to arm and want to support everything there you will need the ability to allocate physical continuous memory for devices (good old DMA).

[Ready4Dis]

It does. Think it over again. With stack you have to do 2^32 pushes, whilst fifo needs 2 or 3 (one for each free entry in E820).

That's wrong. If you have 2^32 bytes of memory, that's 2^20 pages and thus only 2^20 pushes. Filling 4 MB takes much less than a second, once at boot time.
And even if you have to fill 64 MB for a 64 GB RAM server, it's still a matter of less than a few seconds.

1 second in boot times can be very long in embedded systems where boot time requirements is usually very short (boot time requirement of one second is common). This is where that multilevel page allocator comes handy. If you can push sizes of let's say 512MB, the initialization just got much faster. 4GB -> 8 pushes.

You guys are REALLY overstating the time it takes to fill... my system with 4gb it is well under 1s to fill, it's almost not noticeable (haven't timed it however, since it has never been a point of issue). Also, if there was a speific requirement, then it will require a specific adjustment. Don't just say that one algorythm isn't good because in one obscure case if I put this limit on, that it might not work. Either way, 4gb takes well under 1 second, embedded systems tend to have less ram. The benefit is, I have MP and multi tasking initialized BEFORE I start my memory allocator, so as soon as I push a few pages, I can start running other threads without waiting for all of memory to be initialized, reducing start up times to almost nothing. Of course you have to adapt to whatever the specific requirements you are working towards, that's why one solution doens't always fit all. Your method is great in this case, less pushes on startup, but runs slower. For a server that is handling millions of transactions as quickly as possible, it might not be the best solution to bootup a 1/4 of a second faster if it runs slower overall. Other cases, you might require long spans and a bitmap might be the best solution. It obviously depends on the situation, so to try shooting down an implementation based on some obscure, made up, conditions shows ignorance. It's like saying your method is horrible for an 8-bit michrochip due to the low speed (4 clocks per instruction, max speed is only a couple of mhz). Of course you'd pick a solution that either A.) was very fast, or B.) Don't use dynamic memory allocation. So, yes, we can come up with examples to 'prove' a memory allocations scheme isn't always the best in a certain case, but that doesn't make it a horrible solution because you found a case where it may possibly (still not convinced) have to be rethought (like allowing excecution to continue before the entire memory area is full, or only filling up the area's when memory is requested). Everyone is stuck on their own implementation. There is pro's and con's to different implementations, and tricks/tradeoffs to get around situtations... my vote is to use the one that works the best for your situtation. Short on memory? Use a stack. Need contigous allocations? Use a bitmap. Got a small micrcontroller with only 256 bytes of ram, don't even think about using dynamic allocation. Need quick boot up times? Use memory spans, or figure out a way to get around it with the above mentioned methods. I use, and have used every single one of these methods (including no dynamic for my small projects on microchips and avr's), each one has it's merits. My OS currently uses the stack approach for memory > 1mb since at worst case (all memory allocated), it only uses single pointer (whatever the pointer size may be on your platform). It works for me and if I run into an issue that it can't solve, I will find a workaround or switch my algorythm to another type, which isn't hard to do

[mrvn]

Introduction
Every algorithm can be measured in a way that makes it comparable to others by the means on scalability, that's called asymptotic behave. The worst case is, when running time depends on number of input (n), that's theta n, Θ(n). In best case the algorithm has a constant amount of time to run, or we can assume that n has a maximum (therefore we have a max(Θ(n)) deadline), it's Θ(constant). Because I'm lazy, I'll write Θ(1) as 1 is a constant. Walking through a path in a tree for example is Θ(log(n)) as a binary tree of n elements is log(n) tall. That's a typical value, Θ(1) < Θ(log(n)) < Θ(n).

The other important thing is memory footprint. This also scales, so we must know the borders. Worst case when the administrative area size depends on amount of RAM and scales linear, RR(n). Best case (I think you've already figured it out) is to have a constant size, to have a fixed size area indepently on amount of RAM, RR(1).

Armoured with these, let's compare what we have, shall we?

Code: Select all

       |    asymp.    | resource
       +-------+------+ requirement
       | alloc | free | (memory footprint)
-------+-------+--------------------
ideal  |  Θ(1) | Θ(1) | RR(1)
bitmap |  Θ(n) | Θ(n) | RR(n)
stack  |  Θ(1) | Θ(1) | RR(n)          (RR(bitmap)<RR(stack))

Using bitmaps to implement a page allocator is the worst case: scales poorly, and requires large amount of data. The stack school scales very well, but requires even more memory. In an ideal world we would have good scalability and little memory used, but in real life, we have to make compromises. We would be happy if we could allocate pages fast, and we let the free run longer. Free should not scale on number of input, but something else that considerably less will do.

That table is quite full of errors.

Idealy would be not needing any space, so RR(0). A bitmap has O(1) free and a (dynamic) stack or free list has a RR(free pages), meaning the less pages are free the less it uses. Which basically is ideal as it only uses memory when memory is not needed.

[FlashBurn]

A bitmap can also be made O(1) for alloc. You "only" need do divide the bitmaps into smaller chunks. This assumes that you can find a free or set bit in a word in O(1) time. Which is true for x86 cpus.

[Combuster]

Not to mention that Theta(n) isn't the same as O(n): When only a (small) fixed amount of memory is ever allocated, bitmap allocations are constant time. Similarly, heuristics can improve performance such that individual allocations often cost constant time. Both cases disagree with Theta notation because that statement indicates it's asymptotic behaviour is identical to a certain function, essentially stating that allocations must take more time for sufficient increases in size.

A bitmap can also be made O(1) for alloc

Turning a bitmap into a tree stops it from being a bitmap. What you describe is actually known as the buddy allocator.

This assumes that you can find a free or set bit in a word in O(1) time. Which is true for x86 cpus.

Having a practical hardware limit on n doesn't excuse it from being officially O(log n) - and while it's certainly an effective alternative for administrating metadata, knowing that you have to plough through several indirections is certainly going to be slower than the single indirection implied by the stack allocator.


The thing with allocators is that it certainly doesn't paint the entire picture - you often want to have an administration of used memory so that you can implement things like shared library code, and you might to want to have such things integral in your scheme. None of these pure schemes can do used memory management and the theoretical savings of for instance the stack are likely meaningless in the big picture.