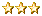Search-optimized bitmap

[Velko]

I've come up with idea about optimized bitmap, which should be able to look up ones (or with slight modifications - zeros) pretty fast.

Begin with bitmap as usual. But then I add another bitmap on top of it and fill it by OR-ing groups of bits of lower level together. If that layer is still too large, I add another level on top of it. Repeat until top-level bitmap is small enough for sequential scan.

Here's an illustration for 64 bits, using 4-bit groups:

bitmap.png (1.7 KiB) Viewed 2533 times

If I set or clear bit, I update bits in upper levels, of course.

Then, if I need to look up a bit, I start from the top, find first bit, move down a level to corresponding group, search there and continue until hit the bottom level.

By my calculations lookup and bit toggling should be O(log_{bits_per_group}(N)).

Ideally I'd use 2-bit groups, thus O(log2(n)), however 8-bit groups (bytes ) seems to be more practical for coding. And O(log8(n)) doesn't seem bad either.

Now, haven't I overlooked something? It almost seems too good to be true

[NickJohnson]

It would be faster to search within each qword linearly, because that only requires one register, but have a tertiary search tree of single bit values to find the proper qword. Essentially, replace the bottom layer with 64 bit values instead of 1 bit ones. Asymptotically, it's still lg4(n).

It's really just a tertiary search tree with only one bit per node, so it does make sense that it's asymptotically lg4(n). Your only problem is that it's hard to store it efficiently without a lot of extra access code if it's not a power of 4 sized bitmap.