I need a big sleeping pill...
I need a big sleeping pill...
Yes, sleepless again...
Anyway, as allways weird things happens in my mind while lying in my bed doing nothing, so here goes: (attachment)
What are your thoughts?
All I know for certain is that if x >= 2 (a natural number that is) the result will aproximately be 1. Of course x cannot equal 0 or 1, nor can x be a negative number (or can it?), however I am uncertain whether or not x has to be a natural number. fx. could x equal pi and still give the same result?
Now that I hopefully have given you something to think about I'll try once again to get some shuteye...
Nighty...
Anyway, as allways weird things happens in my mind while lying in my bed doing nothing, so here goes: (attachment)
What are your thoughts?
All I know for certain is that if x >= 2 (a natural number that is) the result will aproximately be 1. Of course x cannot equal 0 or 1, nor can x be a negative number (or can it?), however I am uncertain whether or not x has to be a natural number. fx. could x equal pi and still give the same result?
Now that I hopefully have given you something to think about I'll try once again to get some shuteye...
Nighty...
- Attachments
-
- doh.png (1.65 KiB) Viewed 1773 times
Last edited by Zacariaz on Sat Mar 22, 2008 7:30 am, edited 1 time in total.
This was supposed to be a cool signature...
- JackScott
- Member

- Posts: 1037
- Joined: Thu Dec 21, 2006 3:03 am
- Location: Hobart, Australia
- Mastodon: https://aus.social/@jackscottau
- Matrix: @JackScottAU:matrix.org
- GitHub: https://github.com/JackScottAU
- Contact:
- Brynet-Inc
- Member

- Posts: 2426
- Joined: Tue Oct 17, 2006 9:29 pm
- Libera.chat IRC: brynet
- Location: Canada
- Contact:
If you add up the first n terms of the formula, it comes to x^0 - x^-1 + x^-1 - x^-2 + x^2 - x^3 + ... + x^(2-n) - x^(1-n) + x^(1-n) - x^-n, and everything except x^0 and x^n cancels out. x^0 is 1, so the first n terms of the formula add up to 1 - 1/x^n. If x > 1 or x < -1, 1/x^n goes to 0 as n goes to infinity, so everything adds up to 1.
If x = 1, 1/x^n is 1, so the sum is 0. If x = -1, 1/x^n alternates between 1 and -1, so the sum alternates between 0 and 2. If -1 < x < 1, the sum is infinite.
If x = 1, 1/x^n is 1, so the sum is 0. If x = -1, 1/x^n alternates between 1 and -1, so the sum alternates between 0 and 2. If -1 < x < 1, the sum is infinite.
Ok, here goes again, but this time I actually have a valid, though stupid, question.
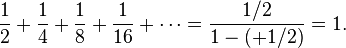
You probably all know this infinite series, but i have never been able to understand how it converges absolutely. When I try to figure it out I just get (2^N - 1)/2^N which is not the same as shown above (I have no idea how someone got to that conclusion by the way) and most certainly doesn't equal 1.
To me the above statement is like saying that 1/3 == .3 Allthough (dependent on the length of the string of 3's) it can be a somewhat precise result, but we all know that isn't the case.
On another note you may notice a certain simularity between this and the one I first posted, so don't say I didn't try.
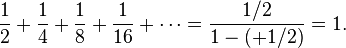
You probably all know this infinite series, but i have never been able to understand how it converges absolutely. When I try to figure it out I just get (2^N - 1)/2^N which is not the same as shown above (I have no idea how someone got to that conclusion by the way) and most certainly doesn't equal 1.
To me the above statement is like saying that 1/3 == .3 Allthough (dependent on the length of the string of 3's) it can be a somewhat precise result, but we all know that isn't the case.
On another note you may notice a certain simularity between this and the one I first posted, so don't say I didn't try.
Last edited by Zacariaz on Sat Mar 22, 2008 7:48 am, edited 1 time in total.
This was supposed to be a cool signature...
- Combuster
- Member

- Posts: 9301
- Joined: Wed Oct 18, 2006 3:45 am
- Libera.chat IRC: [com]buster
- Location: On the balcony, where I can actually keep 1½m distance
- Contact:
the sum will get you here:
1) 1/2 = 1/2
2) 1/2+1/4 = 3/4
3) 1/2+1/4+1/8 = 7/8
n) (2^n)-1 / (2^n)
lets call x (2^n) (to make it easier)
(2^n)-1 / (2^n)
=
x-1 / x
=
x / x - 1 / x
=
1 - 1 / x
=
1 - 1 / (2^n)
=
1 - 2^-n
in other words, one minus a term that gets infinitely small.
now for large n:
lim(n->inf) (1 - 2^-n)
=
lim(n->inf) 1 - lim(n->inf) (2^-n)
=
1 - 0
=
1
hence the sum of 1/2^n converges to 1
1) 1/2 = 1/2
2) 1/2+1/4 = 3/4
3) 1/2+1/4+1/8 = 7/8
n) (2^n)-1 / (2^n)
lets call x (2^n) (to make it easier)
(2^n)-1 / (2^n)
=
x-1 / x
=
x / x - 1 / x
=
1 - 1 / x
=
1 - 1 / (2^n)
=
1 - 2^-n
in other words, one minus a term that gets infinitely small.
now for large n:
lim(n->inf) (1 - 2^-n)
=
lim(n->inf) 1 - lim(n->inf) (2^-n)
=
1 - 0
=
1
hence the sum of 1/2^n converges to 1
I know i converges to 1, of course it does, but i got the impression that it was regarded an absolute and precise result. Maybe I was wrong on that one.Combuster wrote:hence the sum of 1/2^n converges to 1
Anyway, thanks for taking the time, now I have to find something else to bother you with, damnit
edit:
Just got a thought
1/2^N * 2^N/1 = 1
infinity small times infinity large (allthough the infinity could be larger), which is my argument that you shouldn't regards 1/2^n being absolut zero.
On another note we can allso write the result in binary .1111111111... which again isn't 1.
This was supposed to be a cool signature...