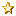How can i stretch bitmaps to fill all of screen

[CrafterMan24]

Hello, everybody!

I wrote a bit-array drawer for my OS

I'm converting bitmaps to bit-arrays in my C program.

Then i'm drawing them with my bit-array drawer. I will write a real BMP loader when i finish ext2 implementation on my os, but currently it is the easiest solution for me.

But i have a problem

I'm drawing bitmap, but resolution can change computer by computer, right?

So i must stretch the bitmap to screen... (decrease or intercase the bitmap size to fill the all of screen with bitmap)

But i don't know how can i do this...

This is a simple array as an example how i save bitmaps:

//A 5 * 3 bitmap:

uint32_t bitmap1[] = {

0, 0xFFFFFF, 0, 0, 0xFEFEFE, // =*==*
0xFFFFFF, 0, 0, 0xFF0F00, 0, // *==*=
0, 0, 0xF0A0F0, 0, 0xFFFFFF // ==*=*

}

Yeah, i store my bitmaps like this...

Then for example i want:

I have an 640*480 bitmap, if the screen resolution 320*200 i want to resize (decrease the size) the bitmap to 320*200, or if the screen resolution is 800*600 i want to resize (intercase the size) the bitmap to 800*600

How can i do that?

Note: Bitmap is 24 bit

Thanks for helping

[iansjack]

If you want to display a bitmap at other than its native resolution then you are going to have to drop some of the pixels or interpolate some extra pixels as the case may be. How you do that is up to you, and what you feel gives the best results. You probably want to work out some way of averaging the pixels rather than just dropping every other one, or doubling every pixel. You'll find a few ideas here: https://en.wikipedia.org/wiki/Image_sca ... algorithms

A fixed-resolution bitmap is probably not the best starting point if you want to display at various resolutions. The most satisfactory solution would be to produce a series of bitmaps one for each resolution that you wish to use; not much good if you want to resize to any size.

[SpyderTL]

If performance isn't a concern, simply convert all of your pixels (int x, int y, byte r, byte g, byte g) into vectors (float x, float y, float r, float g, float b), and scale all of the values from 0.0 to 1.0.

Then build a similar array for your destination pixels.

Then loop through all of your destination pixels, and for each destination pixel, add each source pixel scaled by the inverse distance from the destination pixel. If you adjust the inverse distance formula, you can control the "sharpness" of the final picture, especially if you ignore pixels beyond a certain distance.

This should work for both increasing and decreasing the image size. It's versatile, but slow.

[Brendan]

Hi,

First; do it as 2 steps - horizontal scaling, then vertical scaling.

To scale horizontally, think of each bit in the source as a tiny horizontal line. If the source data is 24 bits wide and the destination data is M pixels wide, then the first bit represents a tiny line from 0 to M/24, the second bit represents a tiny line M/24 to 2*M/24, the third bit represents a line from 2*M/24 to 3*M/24, and so on. With fixed point maths you should be able to generate "8-bit alpha per pixel" relatively easy. For example, with M=66 and "8.8 fixed point", 66/24 = 0x42.00/0x18 = 0x02.C0, which is one whole pixel (alpha = 0xFF) and then a partial pixel (alpha = 0xC0). Note that you probably want to detect runs - e.g. if the source data is 1101111011b then you'd detect 3 runs (one from 0 to 2*M/24, one from 3*M/24 to 7*M/24 and one from 8*M/24 to 10*M/24) and draw 3 small lines (and not 8 tiny lines).

To stretch vertically, calculate how much each "source row of alpha" effects the destination row. For example, if the source data is 32 rows high and the destination is N rows high, then the first source row covers the area from 0 to N/32, the second from N/32 to 2*N/32, the third from 2*N/32 to 3*N/32. With fixed point maths this gives you a weighting factor for each source row. For example; with N = 99 and "8.8 fixed point", 99/32 = 0x63.00/0x20 = 0x03.18, which means the first source row effects the whole first 3 row of the destination data (weighting factor = 0x01.00) and partially effects the fourth row of destination data (weighting factor = 0x00.18). You'd multiply the alpha values from the source row by this weighting factor and add it to the destination data. For example, if the "source row of alpha" is 0x20, 0xFF, 0xFF, 0x60, 0x00 and the weighting factor is 0x00.18 then you'd multiply to get the values 0x03, 0x18, 0x18, 0x09, 0x00 and then add them to the destination row.

Note that a lot of characters share the same "row patterns". For examples; the upper halves of 'O' and 'Q' are the same (and 'B' and 'P', and 'E' and 'F'); a letter like 'I' might be a single bit pattern that's duplicated on most rows; for a letter like 'B' (and 'O', 'E', 'H', etc) the top half is a mirror of the bottom half; etc.

You could store the font data as 2 parts - one part containing "bit pattern for unique row" data, and another part containing the characters where each row of a character is stored as "reference to unique bit pattern". For example, the character 'O' might be stored as "pattern11, pattern12, pattern13, ..., pattern13, pattern12, pattern11" (because its top half is a mirror of its bottom half) and the character 'Q' might be stored as "pattern11, pattern12, pattern13, ..." (because it's top half is the same as the top half of 'O'). With 128 characters that are 32 pixels high; you might only have 200 of these "unique row patterns" (instead of 4096 rows); and you'd scale these 200 "unique row patterns" horizontally (instead of scaling 4096 rows); which saves a whole lot of processing. Also; it can reduce file sizes (if the "reference to unique bit pattern" takes up fewer bits than the "bit pattern for unique row" data, and there's enough characters).

I have done all of this before (but with larger 64*64 fonts). The result (scaled to 2 different sizes) looked like this:



Finally; there's no reason why you can't store the "bit pattern for unique row" data as run-length encoded data. For example, you could have characters that are 254 pixel wide; then have "off width, on width, off width, ..."; where the pattern 000000111111....1111100000000 might be stored as the widths "6, 251, 8, 0xFF" (or just three bytes "6, 251, 0xFF") where the "0xFF" marks the end of the row. This would make it easier/faster to detect runs during the horizontal scaling step (and would also reduce file sizes for wide/high resolution fonts).


Cheers,

Brendan

[gerryg400]

Brendan, this is for 2 colour bit maps only ?

[mallard]

Looks like Brendan didn't even read the question properly, since he's talking about an algorithm specifically for scaling monochrome bitmap fonts when CrafterMan24 was asking about general image scaling and gave example data with 24/32-bit colour (being stuffed into "uint8_t", so dropping the upper 24 bits...).

There are various possible image scaling algorithms, each with their pros/cons. Wikipedia has a good summary (although it focuses on scaling up rather than down). The simplest (and ugliest) option is nearest-neighbour scaling; if you're scaling up a 100px image (line) to 150px, you simply duplicate every second pixel. If you're scaling a 150px image to 100px, you just ignore every third pixel.

Also, if you're looking for easy ways to "embed" images in your source code, checkout the XBM and XPM formats; these can be directly "#include'd" into C or C++ code.

[Brendan]

Hi,

Looks like Brendan didn't even read the question properly, since he's talking about an algorithm specifically for scaling monochrome bitmap fonts when CrafterMan24 was asking about general image scaling and gave example data with 24/32-bit colour (being stuffed into "uint8_t", so dropping the upper 24 bits...).

D'oh - you're right, I thought he was scaling 24-pixel wide fonts, and he's not.

The basic principle is still the same though:

• Scale horizontally first; where each "source pixel" is treated as a tiny line of length "dest_horizontal_resolution / source_horizontal_resolution"; possibly with special case code for simple cases like scaling by integers (where the source pixel is just repeated 2 or more times) and scaling by "reciprocal of integer" (where N source pixels are averaged in an "dest_red = (red1 + red2 + red3 + .... + redN)/N" way).
• Scale vertically; using the same "row weight" stuff from before; possibly with special case code for simple cases like scaling by integers (duplication) and scaling by "reciprocal of integer" (averaging).

Cheers,

Brendan

[Combuster]

Besides, Brendan's font is sufficiently poor to make the difference between È and É illegible at VGA font scale.

[Brendan]

Hi,

Besides, Brendan's font is sufficiently poor to make the difference between È and É illegible at VGA font scale.

You're mistaking "poor font" with "poor DPI". For 10 mm wide by 16 mm tall characters and a 640*480 video mode:

• on a tiny 100 mm wide by 75 mm tall screen the characters end up 64 pixels wide and 100 pixels tall, which is enough "pixels per character" to make fine details very visible
• on a huge 3200 mm wide and 1800 mm tall screen the "exact same physical size" characters end up 2 pixels wide and 4 pixels tall, which is not enough to make any details legible; and for well designed (resolution independent) graphics "bumpy line of smudges" (instead of readable sentences) is perfectly correct. Note that the small characters in that picture are 6*8, and not the 8*16 characters that are typical for VGA text mode.

The only other alternative is to not do scaling; and either have hundreds of hand drawn fonts (one for each permutation of horizontal and vertical size), or to have a single font and get the physical size of characters wrong in almost all cases (e.g. VGA text mode, where physical character size is too small on small screens and too large on large screens).



Cheers,

Brendan

[mallard]

The only other alternative is to not do scaling; and either have hundreds of hand drawn fonts (one for each permutation of horizontal and vertical size), or to have a single font and get the physical size of characters wrong in almost all cases (e.g. VGA text mode, where physical character size is too small on small screens and too large on large screens).

Or have a vector font that's properly hinted for small sizes. Unfortunately, such fonts are fairly rare these days; many of Microsoft's fonts (Arial, Tahoma, Verdana, etc.) are good examples since they've been doing legible text at low resolutions since those low resolutions were considered "high". For open-source/freely distributable fonts, some members of the DejaVu family and the "Liberation" fonts (designed to be replacements for Microsoft's) are correctly hinted.

Unhinted vector fonts look awful at small sizes unless you've got good sub-pixel rendering and a suitably high colour depth and even then tend to look quite "blurry".

[CrafterMan24]

Actually i saw i made a mistake while writing topic, sorry.

My example array's type is uint32_t, not uint8_t...

I will edit now, sorry

[Combuster]

You're mistaking "poor font" with "poor DPI"

Obviously it couldn't be neither the resolution nor pixel size because the VGA itself does an improbably better job at rendering fonts than you would on the exact same hardware.

And besides, I deal with DPI issues for a living so I'd suggest you dispose of whatever gimmick you use to try to read my thoughts. My crystal ball is obviously superior

Note that the small characters in that picture are 6*8, and not the 8*16 characters that are typical for VGA text mode.

Red herring. I had a crack at scaling the large sample down to 8-pixel wide characters. The result is the same: the font is useless, regardless of the many scaling settings I tried. The details are just too small.

[Brendan]

Hi,

Note that the small characters in that picture are 6*8, and not the 8*16 characters that are typical for VGA text mode.

Red herring. I had a crack at scaling the large sample down to 8-pixel wide characters. The result is the same: the font is useless, regardless of the many scaling settings I tried. The details are just too small.

Sure; for one specific font that I wasn't suggesting anyone should use, in an example image intended to show scaling and not the font itself, which I happened to post because that image was already on the forums (and has been since 2009) and was easy to recycle; some of the details were too small for 1987. Should I travel back in time to last Century and start searching for someone that cares?


Cheers,

Brendan