OSDev.org

Samsung's strangely formed screen seems to have fragments with different purposes - maybe you should allow dividing the display into different parts with different names at software level? For example: 640x480@0,0 = "main", 100x100@640,0 = "extra"

NEC's device shouldn't be detected by software. Looks like it's form is distorted to stay comfortable with it's width.

Brendan wrote:For curved screen (e.g. where the distance from eye to screen is constant)

That's an inaccurate description of most curved screens. The curved screens you showed are so wide that the curve is itself intended as a correction from the sides of the screen being too far away for things that assume flat screens.

Other types of curved screens, like the phone example, probably shouldn't have any correction done on them at all, so going through all the trouble of describing them with splines is probably not worth it.

The one that does make sense is the Oculus, which just uses a barrel distortion on both halves of the screen.

I think the most flexible way to describe any screen is shader + parameter.

For normal screen the shader just do bitblt (or with zero-copy tricks) with the screen frame-buffer.
For curve screen like the NEC one, the system may choose a simple transformation shader with proper FOV, preferred view distance and curvature parameters.

With shader you can also get "CGA theme" or grayscale monitor for free

Whatever solution you choose, what happens when we start seeing flexible e-paper displays whose shape can potentially change in real time?

Hi,

Combuster wrote:And even though catmullrom and all the other cardinal splines have the property of each control point actually being touched, they are a liability for various other things. For instance, to make a single corner in the screen, you will want a polygon piece that's exactly horizontally oriented on one side, and exactly vertically oriented on the other side. That means that the control point immediately before and after of the starting point must be horizontal respective to each other, and that the control points immediately before and after the end point are vertical in respect to each other. That leads to a paradoxal situation (taking your middle photo as an example):

Code: Select all

               ^ A must be on this line to avoid bulges :(
               ·
A**/ /*****B** ······> C must be on this line to avoid bulges :(
              * 
               *
               C
               *
               *
               D

I'd hope that, given a set of control points like "(-10,0), (-2, 0), (0, -2), (0, -5)", a correct curve fitting algorithm would give a perfectly horizontal line for "(-10,0) to (-2, 0)", a perfectly round curve with a radius of 2 for "(-2, 0) to (0, -2)" then a perfectly vertical line for "(0, -2), (0, -5)". I'm starting to think that none of the methods of dealing with splines fit my definition of "correct".

Further; I'm wondering if it makes sense to store a "surface normal" for each control point. That way my curve fitting algorithm only needs to care about 2 points (or, for points N and N+1 it doesn't need to care about point N-1 or point N+2). That would also make the curve fitting something that's easily understood (by me):



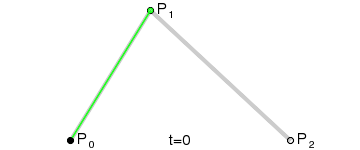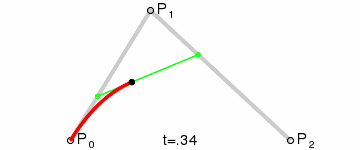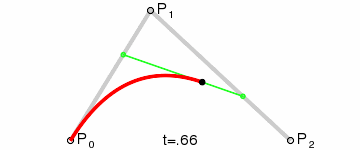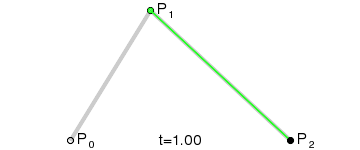
Essentially; I'd be able to have 2 actual control points (P0 and P2 in that diagram) and use the control point's surface normals to find the point of intersection (P1 in that diagram), then generate the curve (which looks like it only involves doing "find the point i% of the way along the line" three times, where i ranges from 0% to 100%).

Combuster wrote:In addition, all the stock B-splines fail if you also want to be able to map actual pixel coordinates correctly, because the plotting coordinate will give the same amount of pixels in A-B as there are in B-C and C-D, or basically, there would mathematically be more pixels in the little screen corner than there is on the primary screen.

Both problems can be fixed by actually specifying the "time" coordinate per spline point, as well as the actual mapping angle. Of course, you can still use the cardinal/catmull-rom equations to suggest initial angles for you and it's probably good to get away with in a fair few cases. You can segment the actual screen in colours to live aid in selecting the actual pixel coordinates, but by now your base mathematical model has already become a non-uniform B-spline

If I split the screen into an arbitrary number of rectangles ("X columns and Y rows") where all columns have a fixed width and all rows have a fixed height; it ends up being a little bit like using sample points to describe a sound wave - by increasing the number of control points you increase the accuracy of the final curve (e.g. that smartphone in the second picture you might have 60 control points on the same straight line followed by 4 that aren't). In this case it's easy to map pixel co-ords correctly because there are the same amount of pixels in A-B as there are in B-C (at least, if you ignore rounding errors - e.g. where you've got 123.5 pixels in A-B and B-C).

However; now I'm thinking you're right; in that it'd make much more sense to split the screen into an arbitrary number of rectangles ("X columns and Y rows") where the columns and rows have arbitrary width/height. This would save space by avoiding pointless control points (e.g. that smartphone in the second picture could be 4 control points instead of "lots of them").

Combuster wrote:There's one problem left: up to now there have only been polynomial splines, and they can't do circles or ellipses, and you will get to see them in practice: B-C above probably is a quarter circle rather than a parabola. To fix that, you need NURBS, and I can imagine a significant bigger portion of programmers running away at this moment.

For a quarter circle; that quadratic bezier curve (the animated diagram above that I mentioned because it's easy for me to understand) would give a parabola. However, with just 3 control points instead of 2 it'd probably approximate a quarter circle with only a small/unnoticeable amount of error (and with more control points the error would be reduced further); and I'm thinking this is probably good enough (especially compared to the error you get from most OSs that assume the screen is flat).

For something that's a lot more complicated (e.g. NURBS); the error might be zero in theory, but you can bet someone (me) will screw it up and the error will be significantly higher in practice.

Note: In theory (assuming 2D for simplicity); a pair of "points with normals" is enough to uniquely describe an ellipse, which means that it's enough to give perfectly round curves (including "quarter circle"). I'm currently researching this (looking for formulas for an ellipse that only uses "points with normals" or "points with tangents" as parameters and not finding one). However, I suspect that this approach will require things like sine, cosine and/or square root (unlike that quadratic bezier curve which doesn't) and will be something I'd prefer to avoid for the sake of performance and/or precision loss.

Combuster wrote:

Brendan wrote:I looked at Catmull-Rom splines, and couldn't figure out how to handle the first and last points correctly.

One of the most common conventions is that the "missing" neighbours of the start and end points are at the same location as the start and end points themselves. And as you have shown, there are sufficient other options and in the end you might just want to deal with it like the problem sketch above.

Originally I assumed that (for Catmull-Rom splines) if the "missing" neighbours of the start and end points are at the same location as the start and end points themselves, then you'd end up with a division by zero or some other "not a number" insanity. I did some research today and I think you're right (in that Catmull-Rom can handle duplicate points if implemented properly).

However; I'm also starting to realise there isn't one correct solution. For example, given 3 points and no other information, there's an infinite number of curves that could all be considered correct, and there is no method (that can be implemented in software) to determine which "correct" set of curves are the curves that were actually intended. Based on this I think more information is required - either adding a lot more control points and/or adding "surface normals" (or tangents, or whatever), and/or adding a way to specify the method to use for generating each individual curve.


Cheers,

Brendan

Hi,

embryo2 wrote:First it is recommended to determine what do you actually need. For what purpose you need the way to describe the curvature? If it should look "so that the video driver could compensate for the curvature in software to ensure that the image the user sees isn't distorted" then the next question is - what kind of distortions you are trying to fight?

In the real world; for each pixel draw a line from the user's eye to that pixel and write down the "altitude and azimuth" angles. Now, in a virtual world do the same - for each pixel draw a line from the camera to that pixel and write down the "altitude and azimuth" angles. For "zero distortion" all of these angles (for all of the pixels) for the virtual world will be identical to the angles in the real world.

Note: I don't care what the "virtual world" is - it could be an immersive 3D game, but it could also be several "application windows" and a few dialog boxes that are floating about in a 3D space.

Owen wrote:I'm not quite sure of the correct approach for this (unless you want to do the scary thing of NURBS, apparently), but while you considered traditional curved screens there, I can think of another class of effectively curved screens to consider, ones that look like this:

For stereoscopic, everything is mostly the same but double (one 2D screen for "left eye" and another 2D screen for "right eye"); and I'd just have 2 displays with 2 different "pixel to location relative to eye" mappings. The part that worries me more about Oculus Rift is that some pixels can't be seen by either eye (there is no "pixel to location relative to eye" mapping), which means that I can use any mapping at all for those areas and waste processing time generating "invisible graphics" or I need to have a way to tell video driver there's no mapping so it can avoid wasting processing time.

embryo2 wrote:(For what its' worth, the correction information for the Oculus Rifts are stored as code - specifically, a fragment shader)

Ideally, I guess I'd be hoping that native video drivers do something similar (e.g. convert the "display shape" data from my display description files into a form that GPU can use, for all different monitor shapes). In practice, it's all going to be done by software running on CPU for the foreseeable future.


Cheers,

Brendan

Hi,

Rusky wrote:

Brendan wrote:For curved screen (e.g. where the distance from eye to screen is constant)

That's an inaccurate description of most curved screens. The curved screens you showed are so wide that the curve is itself intended as a correction from the sides of the screen being too far away for things that assume flat screens.

That doesn't matter much. Normally software generates graphics that is correct for the "flat screen" assumption. When that "correct for flat screen" graphics is displayed on a curved screen it is no longer correct.

Note: I lied (over-simplified). For the typical case where software generates graphics for the "flat screen" assumption and the screen actually is a flat screen; the graphics is only correct if the "field of view" that software used actually matches reality.

Rusky wrote:Other types of curved screens, like the phone example, probably shouldn't have any correction done on them at all, so going through all the trouble of describing them with splines is probably not worth it.

What if I buy 12 of those phones and use a 3*4 grid of phones as my display? Note: To be honest, the curved edge on that phone is a useless annoyance rather than anything practical.

bluemoon wrote:I think the most flexible way to describe any screen is shader + parameter.

For "most flexible" you're probably right. However, for "most practical" I don't think anything that depends on shaders is a viable alternative for my OS (or for any hobby OS).

linguofreak wrote:Whatever solution you choose, what happens when we start seeing flexible e-paper displays whose shape can potentially change in real time?

For flexible screens I'd just use whatever their natural shape is (probably "flat rectangle").


Cheers,

Brendan

Brendan wrote:In the real world; for each pixel draw a line from the user's eye to that pixel and write down the "altitude and azimuth" angles. Now, in a virtual world do the same - for each pixel draw a line from the camera to that pixel and write down the "altitude and azimuth" angles. For "zero distortion" all of these angles (for all of the pixels) for the virtual world will be identical to the angles in the real world.

Your constraint isn't applicable to the situation with different display curvature because it constrains only the real world to virtual world situation for one display. For another display there would be another set of angles, but again, the angles constrain only the real world to virtual world situation, but on a new display.

If you consider the difference between a set of angles for one display and another set of angles for another display then you can catch the distortion a person would see if changing monitors staying in the same position and the picture on both monitors is displayed without any transformation (as is for flat monitors).

I see here a bit different approach can be used. If you imagine a cylinder around you with it's inner surface covered with monitors then I suppose the situation would be close to your idea of a virtual world. Now we can map the image from the cylinder's inner surface to another surface, that can be a surface of a cube around you. And having such mapping allows us to see the same picture on the cube-based display as we can see on the cylinder based. Here is the new constraint emerges that links together any possible monitor configuration with the cylinder based situation. Or you can replace the cylinder with a sphere and create new mapping, but the type of a constraint will be the same - one configuration to another. Even in case of a single flat monitor with a sufficient width it is possible to show the same part of the cylinder/sphere-based picture as if it really was shown on the surrounding surface. Or you can install your flat monitors around you at different distances and still see undistorted world through those "windows", where "undistorted" means that visually the size of a displayable object isn't changed when it moves from one monitor at one distance to another monitor at another distance.

Brendan wrote:Note: In theory (assuming 2D for simplicity); a pair of "points with normals" is enough to uniquely describe an ellipse, which means that it's enough to give perfectly round curves (including "quarter circle"). I'm currently researching this (looking for formulas for an ellipse that only uses "points with normals" or "points with tangents" as parameters and not finding one). However, I suspect that this approach will require things like sine, cosine and/or square root (unlike that quadratic bezier curve which doesn't) and will be something I'd prefer to avoid for the sake of performance and/or precision loss.

If everything is an elliptic arc, then it's never a parabola. Also, try to describe a perfectly flat screen as part of an ellipse

As for your conjecture, its unsolvable for not having sufficient information.

Hi,

embryo2 wrote:

Brendan wrote:In the real world; for each pixel draw a line from the user's eye to that pixel and write down the "altitude and azimuth" angles. Now, in a virtual world do the same - for each pixel draw a line from the camera to that pixel and write down the "altitude and azimuth" angles. For "zero distortion" all of these angles (for all of the pixels) for the virtual world will be identical to the angles in the real world.

Your constraint isn't applicable to the situation with different display curvature because it constrains only the real world to virtual world situation for one display. For another display there would be another set of angles, but again, the angles constrain only the real world to virtual world situation, but on a new display.

If the user surrounds themselves with an eclectic mixture of many different displays (flat, convex, concave, large, small, whatever) the same "angle from eye to any pixel in real world = angle from camera to same pixel in virtual world" should remain true for all pixels in all displays.

To achieve this, each video driver need to know where each pixel is in relation to its display (from my "display description" files) and also needs to know where its display is in relation to the user (from user configuration). Both of these things need to be combined by video driver to construct the "angle from camera to pixel" information that's used during rendering. With multiple displays/video drivers all doing this; you can feed the exact same "virtual world data" (meshes, textures, whatever) to all video drivers, and even though they all handle their own displays individually the end result is perfect distortion free graphics across any number of displays of any type.

Compare this to existing OSs. I have 2 screens, and if I put a window so that it's half on one screen and half on the other then the left half of the window will be a little larger than the right half, the left half will be slightly higher than it should be, and because my monitors are at an angle (in a V shape) the window ends up with a bend in the middle (because its drawn parallel to the screen and not at the correct angle). Note: there's also a minor colour balance problem (the left half of the window will be "slightly less blue and a little more red" than the right half) but that's a separate issue.


Cheers,

Brendan

Hi,

Combuster wrote:

Brendan wrote:Note: In theory (assuming 2D for simplicity); a pair of "points with normals" is enough to uniquely describe an ellipse, which means that it's enough to give perfectly round curves (including "quarter circle"). I'm currently researching this (looking for formulas for an ellipse that only uses "points with normals" or "points with tangents" as parameters and not finding one). However, I suspect that this approach will require things like sine, cosine and/or square root (unlike that quadratic bezier curve which doesn't) and will be something I'd prefer to avoid for the sake of performance and/or precision loss.

If everything is an elliptic arc, then it's never a parabola.

Yes; but if displays are more likely to have elliptic arcs then elliptic arcs would be more useful than parabolas.

Combuster wrote:Also, try to describe a perfectly flat screen as part of an ellipse

As for your conjecture, its unsolvable for not having sufficient information.

That makes choosing between elliptic arcs and parabolic curves easy.


Thanks,

Brendan

Brendan wrote:If the user surrounds themselves with an eclectic mixture of many different displays (flat, convex, concave, large, small, whatever) the same "angle from eye to any pixel in real world = angle from camera to same pixel in virtual world" should remain true for all pixels in all displays.

To achieve this, each video driver need to know where each pixel is in relation to its display (from my "display description" files) and also needs to know where its display is in relation to the user (from user configuration). Both of these things need to be combined by video driver to construct the "angle from camera to pixel" information that's used during rendering. With multiple displays/video drivers all doing this; you can feed the exact same "virtual world data" (meshes, textures, whatever) to all video drivers, and even though they all handle their own displays individually the end result is perfect distortion free graphics across any number of displays of any type.

In case of cylinder/sphere mapping a program needs just two points in real world - the point where an eye is and the point where a pixel is. Next an intersection point is calculated for the line, that connects the mentioned points, and the sphere/cylinder. Next a color is picked from the calculated location on the sphere/cylinder and the screen's pixel is drawn with the picked color.

Now you can compare this very simple algorithm with what will be required for all those altitude and azimuth angles.

Hi,

embryo2 wrote:

Brendan wrote:If the user surrounds themselves with an eclectic mixture of many different displays (flat, convex, concave, large, small, whatever) the same "angle from eye to any pixel in real world = angle from camera to same pixel in virtual world" should remain true for all pixels in all displays.

To achieve this, each video driver need to know where each pixel is in relation to its display (from my "display description" files) and also needs to know where its display is in relation to the user (from user configuration). Both of these things need to be combined by video driver to construct the "angle from camera to pixel" information that's used during rendering. With multiple displays/video drivers all doing this; you can feed the exact same "virtual world data" (meshes, textures, whatever) to all video drivers, and even though they all handle their own displays individually the end result is perfect distortion free graphics across any number of displays of any type.

In case of cylinder/sphere mapping a program needs just two points in real world - the point where an eye is and the point where a pixel is. Next an intersection point is calculated for the line, that connects the mentioned points, and the sphere/cylinder. Next a color is picked from the calculated location on the sphere/cylinder and the screen's pixel is drawn with the picked color.

Now you can compare this very simple algorithm with what will be required for all those altitude and azimuth angles.

You've got a virtual world described by vertices and polygons/triangles. You transform vertices (rotate them about the camera, etc); then clip polygons to the edges of the viewing volume (left/right/top/bottom/near/far planes). Then you use altitude and azimuth angles for each pixel to cast a ray from camera through the pixel and out to the far clipping plane and find the first point where that ray intersects with a polygon/triangle and use that intersection point to determine the colour of the pixel.

If you have "(X, Y, Z) coordinate for the physical location of the pixel", then the only thing it's good for is calculating the altitude and azimuth angles. You don't want to do this calculation for every pixel every frame - you want to do it once, and once you've done it the "(X, Y, Z) coordinates" can be discarded.

Note that casting a ray for each individual pixel has 2 problems - there's no anti-aliasing (unless you cast 2 or more rays per pixel) and it has a lot of overhead.

To really fix the anti-aliasing problem you can find the edges of the pixel and cast a pyramid instead of a ray. This is extremely expensive (but gives very high quality results - equivalent to "infinite super-sampling"). To reduce overhead you can find a horizontal strip of pixels that happen to have the same altitude angle, cast a very wide pyramid (e.g. 300 pixels wide and 1 pixel tall), then sub-divide the resulting horizontal strip (using the azimuth angles).

Also note that for most cases (e.g. flat screen) you won't find a horizontal strip of pixels that have the exact same altitude angles - each pixel's altitude angle will be slightly different to its neighbour by an extremely tiny amount. However, "close enough" is good enough and the pixel's altitude angle only need to extremely similar (e.g. within an allowable tolerance) and not exactly the same.

Of course you could do vertical strips instead of horizontal strips if that gives you larger strips. During initialisation the video driver would determine the angles for each pixel; then determine the most efficient set of vertical and/or horizontal strips.


Cheers,

Brendan

I think of another potentially useful scenario from this topic.

I have a 27" screen, and for this size it's quite common to have non-uniform defect that some area are deemer than other (most likely on edges, but you may also get random factor)

If there is post-processing work before sending frame to display (like shader), this uncomforted defect can be compensated.

If not mentioned before, a simple method for making experiments is just to print a "simulated screenshot" on a paper and bend it according to a simulated viewing device. I am waiting for the photos of this laboratory setup...